Computer vision

We encode each element in a greyscale or RGB matrix (which correspond to a pixel) but individual pixels are impossible to extract information from.

Pixels however have certain properties

This means that we cannot use linear operations (which we have been using, see Linear regression) as:

The image would be flattened into a 1D vector, losing the structure and spatial information of the image. They do not take into account the spatial dependence
The pixels would be processed independently with coefficients applied to each pixel separately as it assumes each pixel is independent of the others, msising important spatial relationships between pixels

This is solved by using Convolution, resulting in a new image $Y$ where each output pixel represents the sum of the product of corresponding image pixel and the filter, $Y = f (X, K)$

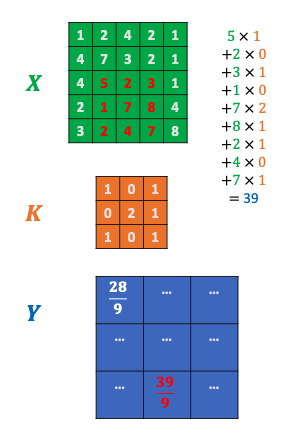
Using convolution

2D matrix $X$ of size $h \times w$ with pixel values $(X_{i, j}) \in [0, 255]$
Convolution kernel $K$ of size $k \times k$ with values $(K_{i, j}) \in R$ , which produces an image $Y$ of size $h^{'} \times w^{'}$ . $k$ is often odd sized

$\forall i \in [1, h^{'}], j \in [1, w^{'}]$ ,

Y_{i, j} = \frac{1}{k^{2}} \sum_{m = 1}^{k} \sum_{n = 1}^{k} X_{i + m - 1, j + n - 1} K_{m, n}

& Weighted average of a pixel and its neighbouring pixels.

2025-03-06_01-20-11_Computer vision_Convolution example.png

$\frac{1}{k^{2}}$ is the normalisation term and is sometimes removed (and we normalise the kernel instead)

# Our convolution function
def convolution(image, kernel):
    # Flip the kernel (optional)
    kernel = np.flipud(np.fliplr(kernel))

    # Get the dimensions of the image and kernel
    image_rows, image_cols = image.shape
    kernel_rows, kernel_cols = kernel.shape

    # Convolve using Numpy
    output = correlate(image, kernel, mode = 'valid')

    # Note that this is equivalent to this
    """
    # Loop through the image, applying the convolution
    output = np.zeros_like(image)
    for x in range(image_rows - kernel_rows + 1):
        for y in range(image_cols - kernel_cols + 1):
            output[x, y] = (kernel * image[x:x+kernel_rows, y:y+kernel_cols]).sum()
    """

    return output

# Display image in matplotlib
plt.imshow(image_conv1, cmap = 'gray')
plt.show()

Flipping the kernel

? Why is the convolution filter flipped in CNN?

Answer here, will revisit someday